Motivation
A propos de la classification des isométries de l’espace hyperbolique, on a deux résultats très connus:
- Premièrement, les isométries de l’espace hyperbolique \(H^{n+1}\) proviennent exactement, via l’extension de Poincaré, de transformations de Möbius de l’espace \(\mathbb R^n\).
- Deuxièmement, les isométries de l’espace \(H^2\) (respectivement \(H^3\)) sont données par \(\mathrm{PGL}(2,\mathbb R)\) (respectivement \(\mathrm{PGL}(2,\mathbb C)\)). De même, les isométries qui préservent l’orientation de l’espace \(H^2\) (respectivement \(H^3\)) sont données par \(\mathrm{PSL}(2,\mathbb R)\) (respectivement \(\mathrm{PSL}(2,\mathbb C)\)).
Les algèbres de Clifford fournissent une manière de généraliser cela aux dimensions supérieures.
Conventions et remarques
- Le terme algèbre désigne pour moi une algèbre associative, unitaire (si, si) et de dimension finie.
- Mon but est de présenter cette construction dans les grandes lignes. Je ne vais pas donner tous les détails car bien des textes le font mieux que moi (voir les références).
Construction – Idée de base
Soit \(V\) un \(K\)-espace vectoriel ainsi que \(Q\) une forme quadratique définie sur \(V\). Pour paraphraser Wikipédia, l’algèbre de Clifford \(Cl(V,Q)\) est l’algèbre (associative et unitaire) engendrée par \(V\) la plus générale qui satisfait \(v\cdot v=Q(v)\cdot 1\) pour tout \(v\) dans \(V\) (je vais probablement omettre bien souvent la multiplication par le \(1\) de l’algèbre).
Remarque (pour casser un peu le suspense): le cas qui va nous intéresser le plus est \(K=\mathbb R\) ainsi que \(Q(x_1,\ldots,x_n)=-{x_1}^2-\ldots-{x_n}^2\). On verra qu’en faisant varier n, on obtiendra successivement les nombres réels, les nombres complexes ainsi que les quaternions de Hammilton.
Construction – Propriété universelle
On peut caractériser l’algèbre de Clifford via une propriété universelle: il s’agit de la donnée d’une algèbre (associative, unitaire) définie sur \(K\) ainsi que d’une application \(K\)-linéaire \(i:V\longrightarrow Cl(V,Q)\) telle que \(i(v)^2=Q(v)\cdot 1\) ; le tout doit satisfaire la propriété universelle suivante
pour toute \(K\)-algèbre \(A\) et toute application \(K\)-linéaire \(f:V\longrightarrow A\) telle que \(f(v)^2=Q(v)\cdot 1_A\), il existe un unique morphisme de \(K\)-alègbres \(\tilde f:Cl(V,Q)\longrightarrow A\) tel que \(\tilde f\circ i = f\):
Ainsi, si l’algèbre de Clifford associée à un couple \((V,Q)\) existe, alors la propriété universelle donne:
- L’algèbre de Clifford \(Cl(V,Q)\) est unique (à isomorphisme près).
- Il s’agit d’un foncteur covariant de la catégorie des \(K\)-espaces vectoriels munis d’une forme quadratique (avec comme morphisme les applications linéaires qui préservent la forme quadratique) dans la catégorie des \(K\)-algèbres (unitaires et associatives).
Construction explicite
On considère pour commencer l’algèbre tensorielle \(T(V)\), c’est-à-dire \(T(V)=\bigoplus_{n=0}^\infty V^{\otimes n}\) et la multiplication dans \(T(V)\) est donnée par le produit tensoriel. Pour terminer, on a plus qu’à considérer l’idéal \(I_Q\) engendré par tous les éléments \(v\otimes v-Q(v,v)\) ainsi que le quotient \(T(V)/I_Q\). Il est alors facile de vérifier la proposition suivante:
Proposition
Le quotient \(T(V)/I_Q\) satisfait la propriété universelle ci-dessus. Ainsi, \(Cl(V,Q)=T(V)/I_Q\).
Une base pour l’algèbre de Clifford
Si \(e_1,\ldots,e_n\) est une \(K\)-base de \(V\), on vérifie que l’ensemble \(\Big\{ e_{i_1}\cdot\ldots\cdot e_{i_k}:1\leq i_1<i_2<\ldots<i_k\leq n\Big\}\) est une base de \(T(V)/I_Q\) (le produit vide est autorisé et correspond au 1). Ainsi, l’algèbre de Clifford \(Cl(V,Q)\) est une algèbre de dimension \(2^{\textrm{dim}_KV}\).
Le cas d’une base orthonormée
Si l’on suppose maintenant \(e_1,\ldots,e_n\) est orthonormée, on obtient les identités:
- \(e_i\cdot e_i=1 \), pour tout i;
- \(e_i\cdot e_j=-e_j\cdot e_i\) pour tous \(i\neq j\).
Dans le prochain article, on verra quelques exemples et où ces algèbres nous mènent…
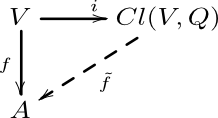
Laisser un commentaire