Il est assez naturel de se demander ce que deviennent les translations de l’espace hyperbolique de dimension n si l’on on travaille dans le modèle de Poincaré (ou modèle conforme). Dans le livre de Ratcliffe (« Foundations of Hyperbolic Manifolds », pour ne pas le nommer), on a la formule suivante: pour tout \(b\in B^n\), la translation s’écrit
\(
\tau_b(x) = \frac{ 1 – |b|^2}{|b|^2\, |x|^2+2x\cdot b+1}x+\frac{|x|^2+2x\cdot b+1}{|b|^2\, |x|^2+2x\cdot b+1}b
\)
Je me demandais si on pouvait voir un peu cette délicate formule. Pour cela, j’ai empoigné Maxima (logiciel de calcul formel, semblable à Mathematica, libre et disponible sous Windows, MacOS et GNU/Linux) et j’ai fait un mini code qui permet de dessiner un arc de courbe et sa translation dans le disque unité:
b: [0.6, 0.6]; F(t):=[0.2*cos(2*%pi*t),0.2*sin(2*%pi*t)]; e1:[1,0]; e2:[0,1]; tau(x):=((1-b.b)/(b.b*x.x+2 * x.b + 1)) * x + ((x.x + 2 * x . b + 1)/(b.b * x.x + 2 * x . b + 1)) * b; plot2d([[parametric, cos(t), sin(t),[t,0,2*%pi], [nticks, 100]],[parametric, F(t).e1, F(t).e2,[t,0,1], [nticks, 100]],[parametric, tau(F(t)).e1, tau(F(t)).e2,[t,0,1], [nticks, 100]]],[legend, false],[box,false],[x,-1,1],[y,-1,1]);
Voici son utilisation:
- La première ligne permet de spécifier le vecteur de translation (il doit avoir une norme strictement inférieure à 1).
- La deuxième ligne permet de donner la courbe à laquelle sera appliquée la translation (ici, un cercle de rayon 0.2). Attention à ce que la courbe reste dans le disque ;-). Elle doit être paramétrisée entre 0 et 1.
Voici quelques exemples (à chaque fois, la courbe originale est en rouge et sa translation en vert):

F(t):=[0.2*cos(2*%pi*t),0.2*sin(2*%pi*t)];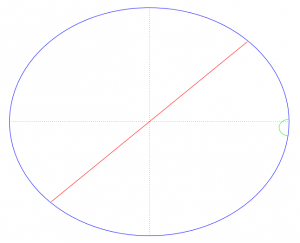
F(t):=[t*1.4-0.7,t*1.4-0.7];
Laisser un commentaire